MySQL 索引梳理

底层数据结构选型

Hash

缺点：哈希索引不支持顺序和范围查询。

哈希表可以通过接近 O(1) 的时间复杂度在键值对集合中快速检索数据。通过哈希算法（散列算法），可以快速找到key对应的index，找到了index也就找到了对应的value。但是哈希算法存在哈希冲突问题，一般通过增加链表来解决哈希冲突（JDK1.8以后引入了红黑树）。

但是 MySQL 的哈希索引是经过改造的，称为自适应哈希索引。这种哈希索引的哈希桶是一个小型的B+ 树。这个 B+ 树可以存储多个键值对，而不是一个键，这有助于减少冲突链的长度，提高查询效率。

试想一种情况  SELECT * FROM tb1 WHERE id < 500 ，在这种范围查询中，B+ 树优势非常大，直接遍历比 500 小的叶子节点就可以完成。

二叉查找树

缺点：二叉查找树的性能非常依赖于它的平衡程度，不稳定。

二叉查找树（Binary Search Tree）是一种基于二叉树的数据结构，它具有以下特点：

1. 左子树所有节点的值均小于根节点的值。

2. 右子树所有节点的值均大于根节点的值。

3. 左右子树也分别为二叉查找树。

   

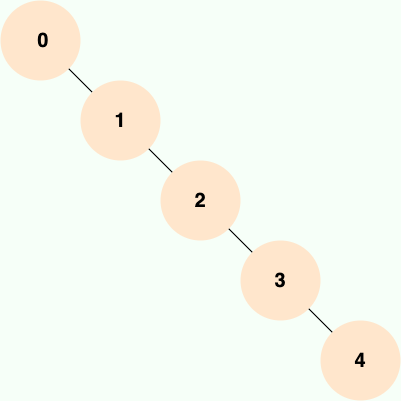
当二叉查找树是平衡的时候，也就是树的每个节点的左右子树深度相差不超过 1 的时候，查询的时间复杂度为 O(log(N))，具有比较高的效率。然而，当二叉查找树不平衡时，例如在最坏情况下（有序插入节点），树会退化成线性链表（也被称为斜树），导致查询效率急剧下降，时间复杂退化为 O（N）。

也就是说，二叉查找树的性能非常依赖于它的平衡程度，这就导致其不适合作为 MySQL 底层索引的数据结构。

为了解决这个问题，并提高查询效率，人们发明了多种在二叉查找树基础上的改进型数据结构，如平衡二叉树、B-Tree、B+Tree 等。

AVL 树

缺点：需要多次旋转操作保持平衡，IO 次数多。

由于 AVL 树需要频繁地进行旋转操作来保持平衡，因此会有较大的计算开销进而降低了数据库写操作的性能。并且， 在使用 AVL 树时，每个树节点仅存储一个数据，而每次进行磁盘 IO 时只能读取一个节点的数据，如果需要查询的数据分布在多个节点上，那么就需要进行多次磁盘 IO。 磁盘 IO 是一项耗时的操作，在设计数据库索引时，我们需要优先考虑如何最大限度地减少磁盘 IO 操作的次数。

红黑树

缺点：平衡性弱，获取某些数据需要多次 IO 操作。

红黑树并不追求严格的平衡，而是大致的平衡。正因如此，红黑树的查询效率稍有下降，因为红黑树的平衡性相对较弱，可能会导致树的高度较高，这可能会导致一些数据需要进行多次磁盘 IO 操作才能查询到，这也是 MySQL 没有选择红黑树的主要原因。也正因如此，红黑树的插入和删除操作效率大大提高了，因为红黑树在插入和删除节点时只需进行 O(1) 次数的旋转和变色操作，即可保持基本平衡状态，而不需要像 AVL 树一样进行 O(logn) 次数的旋转操作。

B+ 树和 B 树

• B Tree：每个结点既存储 key 又存储 data，数据分布在所有结点。
• B+ Tree：所有 data 只存储在叶子结点，非叶子节点只存储 key 用于导航，叶节点是双向链表。

为什么用 B+树不用 B 树

• 范围查询更高效：在 B 树中进行范围查询时，首先找到要查找的下限，然后对 B 树进行中序遍历，直到找到查找的上限；而 B+树的范围查询，只需要对链表进行遍历即可。
• 磁盘 IO 更快：B 树的所有节点既存放键(key) 也存放数据(data)，而 B+树只有叶子节点存放 key 和 data，其他内节点只存放 key。
• 检索稳定程度：B 树的检索的过程相当于对范围内的每个节点的关键字做二分查找，可能还没有到达叶子节点，检索就结束了。而 B+树的检索效率很稳定，任何查找都是从根节点到叶子节点的过程，叶子节点的顺序检索很明显。

综上，B+树与 B 树相比，具备更少的 IO 次数、更稳定的查询效率和更适于范围查询这些优势。

聚簇索引、非聚簇索引和回表查询

聚簇索引

聚簇索引（Clustered Index）通常与主键索引相关联（如果存在主键索引的话）。如果一张表中显式定义了主键，那么在这表中我们可认为主键索引等价于聚簇索引。在 InnoDB 存储引擎中，聚簇索引使用 B+ 树实现，其叶子节点直接存储了行数据，而不是存储行数据的内存地址。这意味着，通过聚簇索引，我们可以直接访问到存储在磁盘上的行数据，而不需要额外的查找步骤。这种设计使得聚簇索引在数据检索时非常高效，因为它减少了数据访问时的 I/O 操作。如果没有显式定义主键，InnoDB 会使用一个非空的唯一索引作为聚簇索引；如果没有这样的唯一索引，InnoDB会隐式创建一个包含所有行的隐藏聚簇索引。

由于聚簇索引是将数据和索引放在一起的，因此 一张表仅有一个聚簇索引。

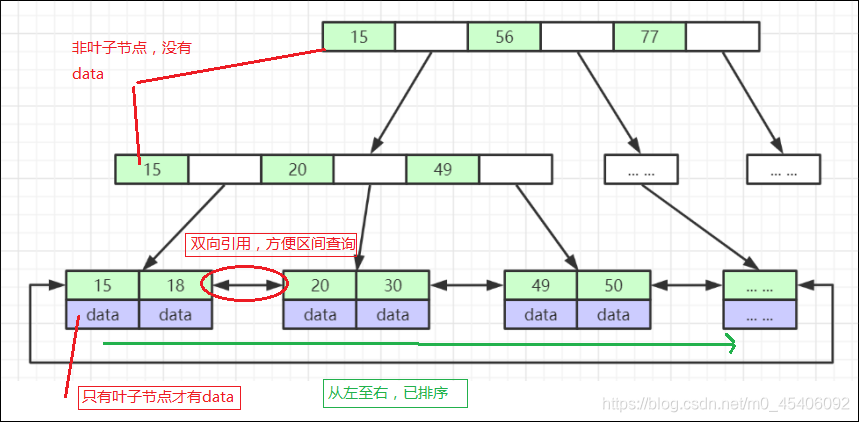
非聚簇索引和回表查询

在非聚簇索引的叶子节点上存储的并不是真正的行数据，而是主键 ID，所以当我们使用非聚簇索引进行查询时，首先会得到一个主键 ID，然后再使用主键 ID 去聚簇索引上找到真正的行数据，我们把这个过程称之为回表查询。

覆盖索引和联合索引

覆盖索引

覆盖索引即需要查询的字段正好是索引的字段，那么直接根据该索引，就可以查到数据了，而无需回表查询。如主键索引，如果一条 SQL 需要查询主键，那么正好根据主键索引就可以查到主键。再比如普通索引，如果一条 SQL 需要查询 name，name 字段正好有索引，那么直接根据这个索引就可以查到数据，也无需回表。

联合索引

使用表中的多个字段创建索引，就是 联合索引，也叫 组合索引 或 复合索引。以 score 和 name 两个字段建立联合索引：ALTER TABLE cus_order ADD INDEX id_score_name(score, name);

最左前缀匹配

最左匹配原则就是指在联合索引中，如果你的 SQL 语句条件中用到了联合索引中的最左边的一列或连续几列，那么这条 SQL 语句就可以利用这个联合索引去进行匹配，提高了查询效率。

最左匹配原则会一直向右匹配，直到遇到范围查询（如 >、<）为止。对于 >=、<=、BETWEEN 以及前缀匹配 LIKE 的范围查询，不会停止匹配。

如果有索引 联合索引（a，b，c），查询 a=1 AND c=1会走索引么？c=1 呢？b=1 AND c=1呢？

• 查询 a=1 AND c=1：根据最左前缀匹配原则，查询可以使用索引的前缀部分。因此，该查询仅在 a=1 上使用索引，然后对结果进行 c=1 的过滤。
• 查询 c=1 ：由于查询中不包含最左列 a，根据最左前缀匹配原则，整个索引都无法被使用。
• 查询b=1 AND c=1：和第二种一样的情况，整个索引都不会使用。

正确使用索引

• 选择合适字段创建索引：一般在不为NULL，不会频繁被查询/操作/链接/排序的字段上建立索引
• 被频繁更新的字段要慎重建立索引：因为索引的维护成本很大
• 限制每张表上的索引数量：如果每张表上有多个索引可用，会增加MySQL优化器生成执行计划的时间，降低查询性能。
• 尽量考虑联合索引而不是单列索引
• 字符串类型的字段使用前缀索引代替普通索引

索引失效

1. 不满足最左前缀匹配原则
2. 错误的模糊查询：只有 like %字符串 会走索引，其他形式的模糊查询都不走索引
3. 索引列运算： where id + 1 = 2 不会走索引， where id = 1 会走索引
4. 使用函数： where ifnull(id, 0) = 1 不会走索引
5. 类型转换： where address = '123' 会走索引， where address = 123 不会走索引

B+ Tree 索引查找的页级 IO

1. B+ 树的“扇出”（Fan-out）

• 每个内部节点页存储 键 + 子页指针。假设主键为 8 字节，页指针（文件地址）也是 8 字节，一对键指针共 16 B。
• 16 KB 的页，大致可放： 16 KB / 16B = 1024 个 entry
• 这个 扇出 数是指每个内部节点最多可分叉 1000 份。

2. 树高（Depth）估算

3. 读页 I/O 次数

• 层 1：读取根节点页
• 层 2：读取中间节点页
• 层 3：读取叶子节点页（叶子页中存有实际记录的物理位置）
• 对于 主键索引（Clustered Index）：叶子节点即是数据页，无需额外 I/O
• 对于 二级索引（Secondary Index）：叶子页存储主键，然后还要一次数据页随机读，再 +1 次 I/O

索引类型	需读页层数	额外的数据页 I/O	总 I/O
主键索引	根 + 中间 + 叶子 = 3 次	0	3 次
二级索引	根 + 中间 + 叶子 = 3 次	+1 次	4 次